Modelos Lineales

Seguimos usando la data del artículo:

Holland, Alisha C., and José Incio. 2018. “Imperfect Recall: The Politics of Subnational Office Removals.” Comparative Political Studies: 0010414018797939.

library(rio)
recall<-import("https://github.com/jincio/Imperfect_recall/raw/master/recalldataset.dta")

0.1 Modelo Lineal

m1<-lm(enp~indigenous+execution, data=recall)
summary(m1)

## 
## Call:
## lm(formula = enp ~ indigenous + execution, data = recall)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.5745 -1.0383 -0.2044  0.8683  6.9390 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  4.81361    0.14090  34.163  < 2e-16 ***
## indigenous   0.49014    0.06096   8.041 1.11e-15 ***
## execution   -0.87338    0.18216  -4.795 1.68e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.422 on 4875 degrees of freedom
##   (1680 observations deleted due to missingness)
## Multiple R-squared:  0.01875,    Adjusted R-squared:  0.01834 
## F-statistic: 46.57 on 2 and 4875 DF,  p-value: < 2.2e-16

m1<-lm(enp~indigenous+execution*incumbent, data=recall)
summary(m1)

## 
## Call:
## lm(formula = enp ~ indigenous + execution * incumbent, data = recall)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.6358 -1.0178 -0.1940  0.8399  6.7714 
## 
## Coefficients:
##                     Estimate Std. Error t value Pr(>|t|)    
## (Intercept)          4.88294    0.15498  31.508  < 2e-16 ***
## indigenous           0.35990    0.06095   5.905 3.78e-09 ***
## execution           -0.74652    0.20129  -3.709 0.000211 ***
## incumbent           -0.47384    0.34205  -1.385 0.166017    
## execution:incumbent -0.20172    0.44427  -0.454 0.649816    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.4 on 4873 degrees of freedom
##   (1680 observations deleted due to missingness)
## Multiple R-squared:  0.04873,    Adjusted R-squared:  0.04795 
## F-statistic: 62.41 on 4 and 4873 DF,  p-value: < 2.2e-16

0.2 Robust Estandard Errors

library(lmtest)

## Loading required package: zoo

## 
## Attaching package: 'zoo'

## The following objects are masked from 'package:base':
## 
##     as.Date, as.Date.numeric

library(sandwich)
coeftest(m1, vcov = vcovHC(m1, "HC0")) 

## 
## t test of coefficients:
## 
##                      Estimate Std. Error t value  Pr(>|t|)    
## (Intercept)          4.882936   0.158289 30.8483 < 2.2e-16 ***
## indigenous           0.359900   0.061191  5.8816 4.334e-09 ***
## execution           -0.746516   0.205095 -3.6399 0.0002756 ***
## incumbent           -0.473845   0.320293 -1.4794 0.1390958    
## execution:incumbent -0.201720   0.410768 -0.4911 0.6233912    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

En este post damos más detalles de cómo agregar los robust standard errors en el resultados de nuestro modelo. Aquí

0.3 Diagnostico

0.3.1 Valores influyentes

library(car)

## Loading required package: carData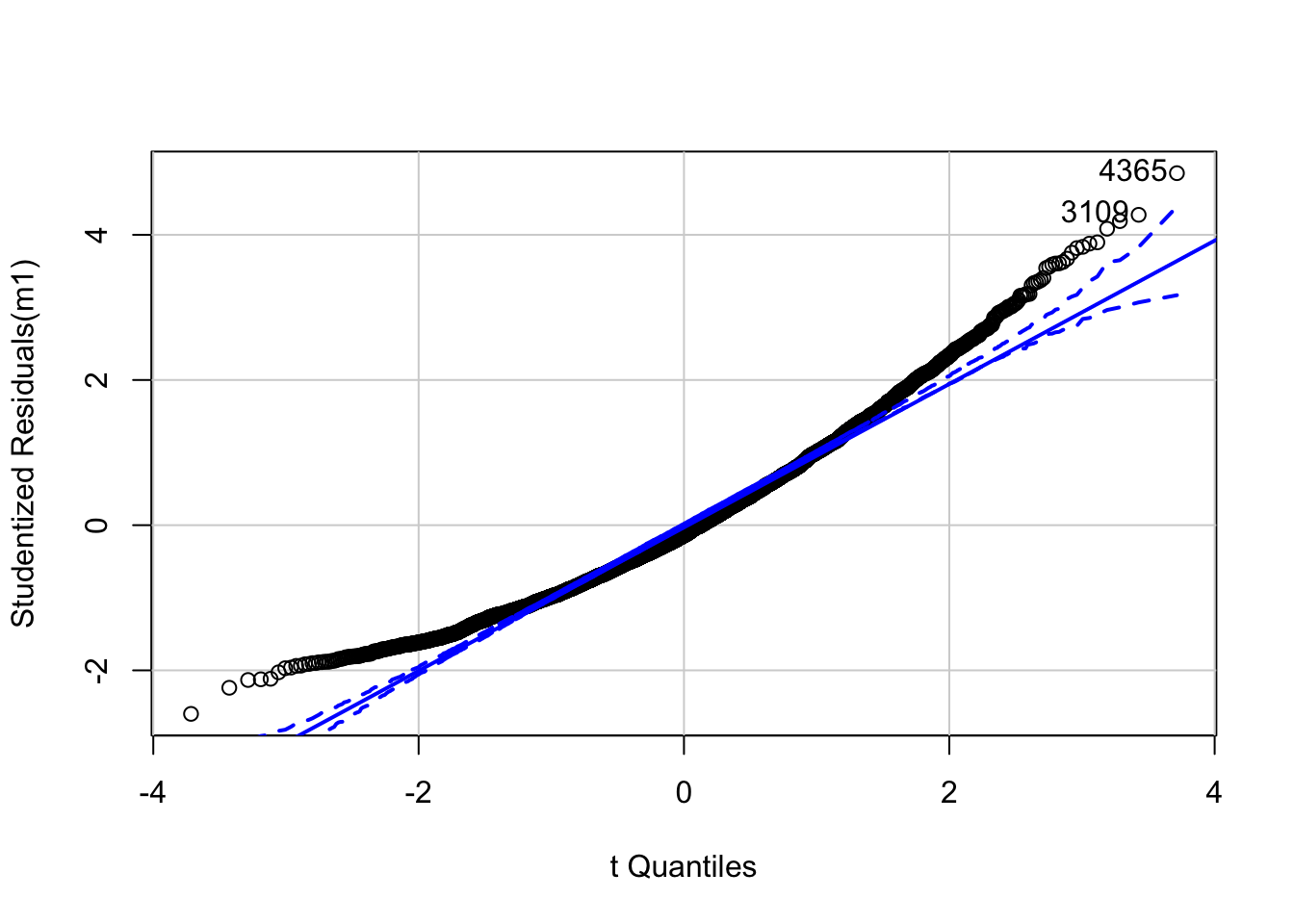

qqPlot(m1)

## [1] 3109 4365

outlierTest(m1) 

##      rstudent unadjusted p-value Bonferroni p
## 4365 4.849204         1.2782e-06    0.0062349

0.3.2 Multicolinealidad

vif(m1)

##          indigenous           execution           incumbent 
##            1.035507            1.264523           47.105976 
## execution:incumbent 
##           47.641679

sqrt(vif(m1)) > 2 

##          indigenous           execution           incumbent 
##               FALSE               FALSE                TRUE 
## execution:incumbent 
##                TRUE

0.3.3 Normalidad de los residuos

Creamos un objeto que contenga los valores residuales del modelo, con la finalidad de probar si los residuos tienen una distribución normal. De no tenerla, sería problemático al momento de inferir.

res<-residuals(m1)

library(nortest)
sf.test(res)

## 
##  Shapiro-Francia normality test
## 
## data:  res
## W = 0.97099, p-value < 2.2e-16

ad.test(res)

## 
##  Anderson-Darling normality test
## 
## data:  res
## A = 31.417, p-value < 2.2e-16

0.3.4 Homocedasticidad

fit<-fitted.values(m1)
scatterplot(fit,res)

spreadLevelPlot(m1)

## 
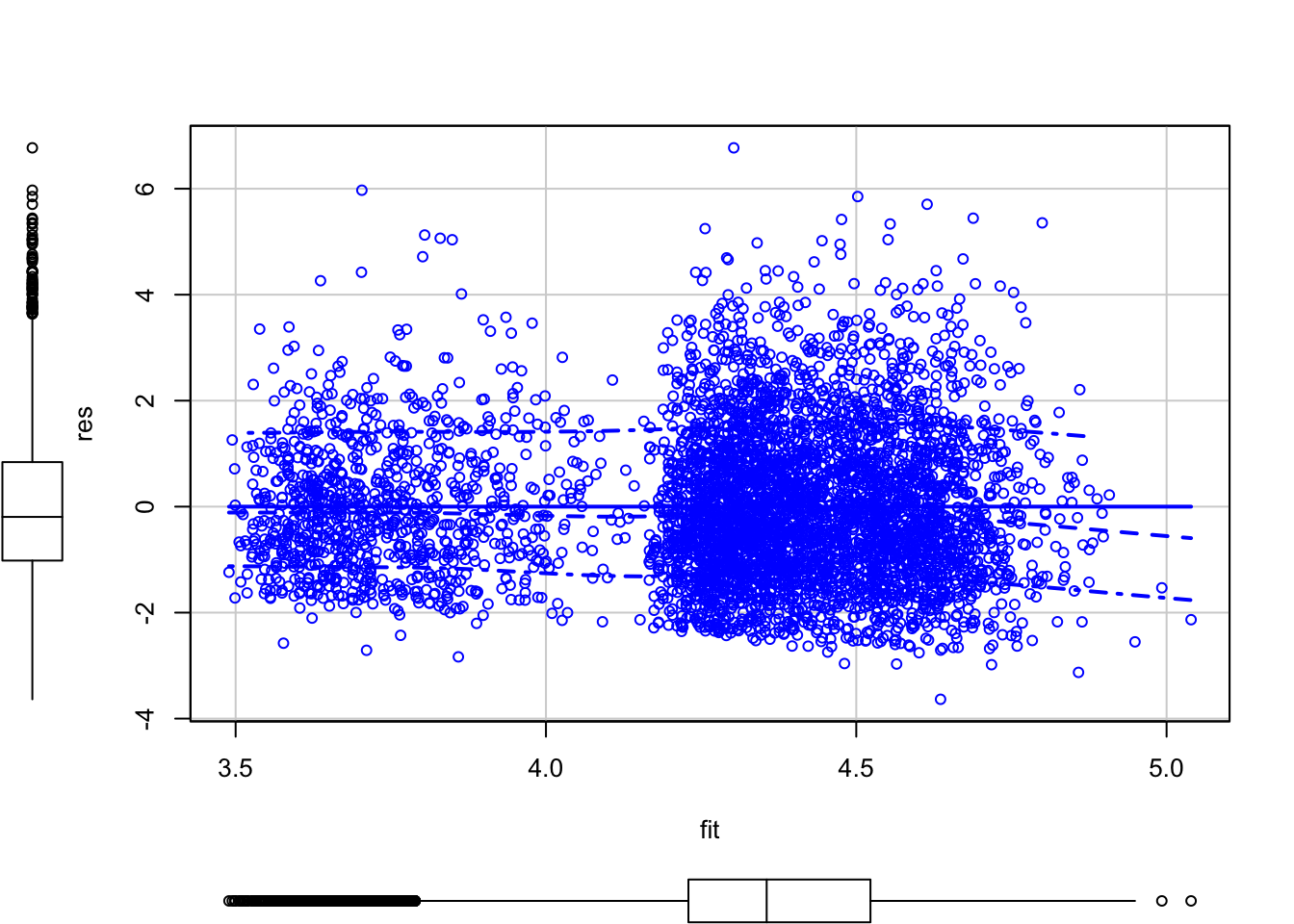
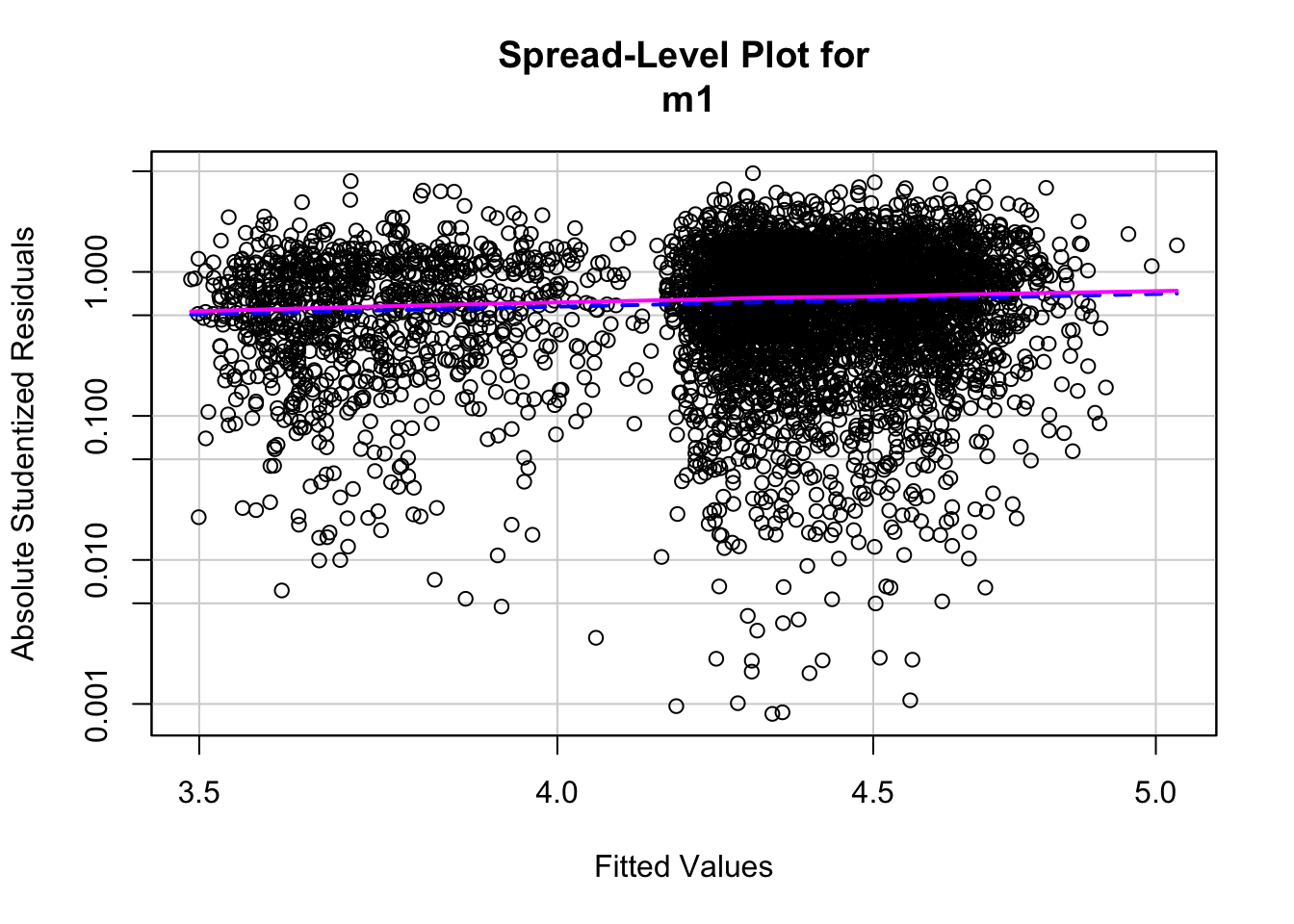
## Suggested power transformation:  0.09177957

library(lmtest)
bptest(m1)

## 
##  studentized Breusch-Pagan test
## 
## data:  m1
## BP = 28.356, df = 4, p-value = 1.056e-05

par(mfrow=c(2,2))
plot(m1)